Page 86 - 70

яка є меншою від дисперсії будь-якої іншої лінійної оцінки. Таким
чином x є також і ефективною оцінкою математичного сподівання
випадкової величини.
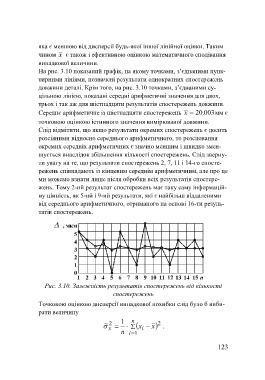
На рис. 3.10 показаний графік, на якому точками, з’єднаними пунк-
тирними лініями, позначені результати однократних спостережень
довжини деталі. Крім того, на рис. 3.10 точками, з’єднаними су-
цільною лінією, показані середні арифметичні значення для двох,
трьох і так аж для шістнадцяти результатів спостережень довжини.
Середнє арифметичне із шістнадцяти спостережень x  20, 003мм є
точковою оцінкою істинного значення вимірюваної довжини.
Слід відмітити, що якщо результати окремих спостережень є досить
розсіяними відносно середнього арифметичного, то розсіювання
окремих середніх арифметичних є значно меншим і швидко змен-
шується внаслідок збільшення кількості спостережень. Слід зверну-
ти увагу на те, що результати спостережень 2, 7, 11 і 14-го спосте-
режень співпадають із кінцевим середнім арифметичним, але про це
ми можемо взнати лише після обробки всіх результатів спостере-
жень. Тому 2-ий результат спостережень має таку саму інформацій-
ну цінність, як 5-ий і 9-ий результати, які є найбільш віддаленими
від середнього арифметичного, отриманого на основі 16-ти резуль-
татів спостережень.



Рис. 3.10. Залежність результатів спостережень від кількості
спостережень
Точковою оцінкою дисперсії випадкової похибки слід було б виби-
рати величину
n
~ 2
 x  1   x i   x 2 .
n  i 1
123