Page 32 - 6832

Розглянемо ряд вибіркових значень х 1,х 2,...,х п випадкової величини X. Позначимо п х – кількість
n
значень, що перебуває ліворуч від вибраного значення. Тоді відношення x  W n (x ) і є емпіричною
n
функцією розподілу. При великому обсязі вибірки емпірична функція розподілу W n(х) є
апроксимацією теоретичної функції розподілу F(x).
x
F( x)   p( x) dx
 
Різниця величин W n (x) і F(x) може бути використана як міра розбіжності між вибірковими
даними та передбачуваним законом розподілу генеральної сукупності. За міру цієї розбіжності
беруть середній квадрат відхилень за всіма можливими значеннями аргументу:

2
 2  [W n (x )  (xF )] dF (x )

 
де dF( x)  F (  x) dx
З наявних вибіркових даних будується варіаційний ряд < < ⋯ < . Теоретично рівність

будь-яких двох членів у цьому ряді через неперервність функції F(х) практично неможлива, тобто
має ймовірність, що дорівнює нулю. Вважаємо, що для х<x 1 емпірична функція розподілу дорівнює
нулю, а при х>х п , дорівнює одиниці. Відповідно до такого визначення функції W n (x) маємо:
W ( x)  ,0 x  x 1
n

 k
 W ( x)  x , 1  x  x , k  2,1 ,..., n 1 (2.14)
n
k
 n
W ( x)  ,1 x  x n

n
1
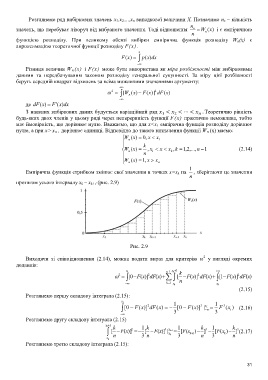
Емпірична функція стрибком змінює свої значення в точках x=x k на , зберігаючи це значення
n
протягом усього інтервалу x k – x k+1 (рис. 2.9)

Рис. 2.9

2
Виходячи зі співвідношення (2.14), можна подати вираз для критерію ω у вигляді окремих
доданків:
1 x n 1 k 1 k 
x
2
2
2

 2  0[  (xF )] dF (x  )   [  (xF )] dF (x )  1[  (xF )] dF (x )

  k 1 x k n x k
(2.15)
Розглянемо першу складову інтеграла (2.15):
1 x 1 1
2
| 
 0 [  F (x )] dF (x )   0 [  F (x )] 3 x i  F 3 (x i ) (2.16)

  3 3
Розглянемо другу складову інтеграла (2.15)
1 
x k
k 2 1 k 1 k 3 1 k 3
| 
 [  F (x )]   [  F (x )] 3 x k 1 [F (x k 1 ) ]  [F (x k ) ] (2.17)
x k
n 3 n 3 n 3 n
x k
Розглянемо третю складову інтеграла (2.15):
31