Page 25 - 6831

Лекція 5. Основи однофакторного регресійного аналізу

План:
1. Точкова оцінка параметрів лінійного рівняння регресії за методом найменших
квадратів.
2. Коефіцієнт регресії та його зв’язок з коефіцієнтом кореляції.
3. Перевірка гіпотези про наявність лінійного кореляційного зв’язку.
4. Інтервальні оцінки параметрів лінійної регресії та лінії регресії.
5. Порівняння двох лінійних рівнянь регресій.

Регресійний аналіз (лат. regressio – рух назад) – розділ мамематичної статистики, що
вивчає математичне моделювання залежності середнього значення результативної ознаки від
одної або декількох факторних ознак з наступною статистичною оцінкою якості моделі.У
випадку одної факторної ознаки регресійний аналіз називають однофакторним.
Нехай кореляційний зв’язок між результативною ознакою Y і фактором Х описується
лінійним рівнянням регресії:

= Ах + В, (1)
х

де - умовне середнє арифметичне значення ознаки Y для заданого значення ознаки Х=х;
х
А; В - математичне сподівання параметрів рівняння регресії, точкові оцінки яких аі
bпроводиться за допомогою вибірки об’ємом n методом найменших квадратів (МНК).
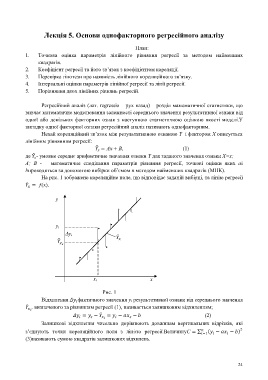
На рис. 1 зображено кореляційне поле, що відповідає заданій вибірці, та лінію регресії

= ƒ(х).

.
у
. .

. . .
у і .
у і

. = +

.
. .

х і x

Рис. 1
Відхилення фактичного значення у і результативної ознаки від середнього значення

, визначеного за рівнянням регресії (1), називається залишковим відхиленням;

= − = − − (2)

Залишкові відхилення чисельно дорівнюють довжинам вертикальних відрізків, які

з’єднують точки кореляційного поля з лінією регресії.ВеличинуС = ∑ ( − − )

(3)називають сумою квадратів залишкових відхилень.
24