Page 65 - 6769

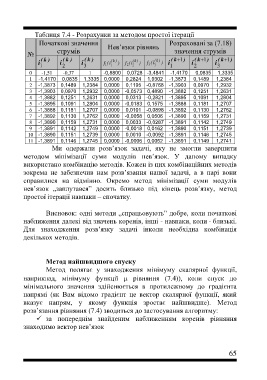
Таблиця 7.4 - Розрахунки за методом простої ітерації
Початкові значення Нев’язки рівнянь Розраховані за (7.18)
№ струмів значення струмів
i ( k ) i ( k ) i ( k ) i ( f ) k ( ) f i ( ) k ( ) f i ( ) k ( ) i ( k+ ) 1 i ( k+ ) 1 i ( k+ ) 1
1 2 3 1 1 2 2 3 3 1 2 3
0 -1,51 -0,37 1 -0,8800 0,0728 -3,4841 -1,4170 0,0835 1,3335
1 -1,4170 0,0835 1,3335 0,0000 0,2824 1,9302 -1,3873 0,1489 1,2384
2 -1,3873 0,1489 1,2384 0,0000 0,1195 -0,8768 -1,3903 0,0970 1,2932
3 -1,3903 0,0970 1,2932 0,0000 -0,0573 0,4890 -1,3882 0,1251 1,2631
4 -1,3882 0,1251 1,2631 0,0000 0,0313 -0,2821 -1,3895 0,1091 1,2804
5 -1,3895 0,1091 1,2804 0,0000 -0,0183 0,1575 -1,3888 0,1181 1,2707
6 -1,3888 0,1181 1,2707 0,0000 0,0101 -0,0898 -1,3892 0,1130 1,2762
7 -1,3892 0,1130 1,2762 0,0000 -0,0058 0,0506 -1,3890 0,1159 1,2731
8 -1,3890 0,1159 1,2731 0,0000 0,0033 -0,0287 -1,3891 0,1142 1,2749
9 -1,3891 0,1142 1,2749 0,0000 -0,0018 0,0162 -1,3890 0,1151 1,2739
10 -1,3890 0,1151 1,2739 0,0000 0,0010 -0,0092 -1,3891 0,1146 1,2745
11 -1,3891 0,1146 1,2745 0,0000 -0,0006 0,0052 -1,3891 0,1149 1,2741
Ми одержали розв’язок задачі, яку не змогли завершити
методом мінімізації суми модулів нев’язок. У даному випадку
використано комбінацію методів. Кожен із цих комбінаційних методів
зокрема не забезпечив нам розв’язання нашої задачі, а в парі вони
справилися на відмінно. Окремо метод мінімізації суми модулів
нев’язок „заплутався” досить близько під кінець розв’язку, метод
простої ітерації навпаки – спочатку.

Висновок: одні методи „спрацьовують” добре, коли початкові
наближення далекі від значень коренів, інші - навпаки, коли - близькі.
Для знаходження розв’язку задачі інколи необхідна комбінація
декількох методів.

Метод найшвидшого спуску
Метод полягає у знаходження мінімуму скалярної функції,
наприклад, мінімуму функції  рівняння (7.4)), коли спуск до
мінімального значення здійснюється в протилежному до градієнта
напрямі (як Вам відомо градієнт це вектор скалярної функції, який
вказує напрям, у якому функція зростає найшвидше). Метод
розв’язання рівняння (7.4) зводиться до застосування алгоритму:
✓ за попереднім знайденим наближенням коренів рівняння
знаходимо вектор нев’язок

65