Page 63 - 6769

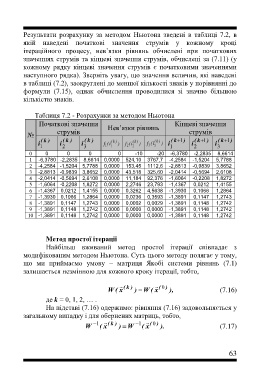
Результати розрахунку за методом Ньютона зведені в таблиці 7.2, в
якій наведені початкові значення струмів у кожному кроці
ітераційного процесу, нев’язки рівнянь обчислені при початкових
значеннях струмів та кінцеві значення струмів, обчислені за (7.11) (у
кожному рядку кінцеві значення струмів є початковими значеннями
наступного рядка). Зверніть увагу, що значення величин, які наведені
в таблиці (7.2), заокруглені до меншої кількості знаків у порівнянні до
формули (7.15), однак обчислення проводилися зі значно більшою
кількістю знаків.

Таблиця 7.2 - Розрахунки за методом Ньютона
Початкові значення Нев’язки рівнянь Кінцеві значення
№ струмів струмів
i 1 ( k ) i 2 ( k ) i 3 ( k ) 1 i ( f 1 ) k ( ) f 2 i ( 2 ) k ( ) f 3 i ( 3 ) k ( ) i 1 ( k+ ) 1 i ( 2 k ) 1 + i 3 ( k+ ) 1

0 0 0 0 0 -10 -20 -6,3780 -2,2835 8,6614
1 -6,3780 -2,2835 8,6614 0,0000 524,10 3767,7 -4,2584 -1,5204 5,7788
2 -4,2584 -1,5204 5,7788 0,0000 153,45 1112,6 -2,8813 -0,9839 3,8652
3 -2,8813 -0,9839 3,8652 0,0000 43,518 325,60 -2,0414 -0,5694 2,6108
4 -2,0414 -0,5694 2,6108 0,0000 11,184 92,376 -1,6064 -0,2208 1,8272
5 -1,6064 -0,2208 1,8272 0,0000 2,2746 23,793 -1,4367 0,0212 1,4155
6 -1,4367 0,0212 1,4155 0,0000 0,3262 4,5638 -1,3930 0,1066 1,2864
7 -1,3930 0,1066 1,2864 0,0000 0,0236 0,3593 -1,3891 0,1147 1,2743
8 -1,3891 0,1147 1,2743 0,0000 0,0002 0,0029 -1,3891 0,1148 1,2742
9 -1,3891 0,1148 1,2742 0,0000 0,0000 0,0000 -1,3891 0,1148 1,2742
10 -1,3891 0,1148 1,2742 0,0000 0,0000 0,0000 -1,3891 0,1148 1,2742

Метод простої ітерації
Найбільш вживаний метод простої ітерації співпадає з
модифікованим методом Ньютона. Суть цього методу полягає у тому,
що ми приймаємо умову – матриця Якобі системи рівнянь (7.1)
залишається незмінною для кожного кроку ітерації, тобто,

 
W ( x ( k ) ) = W ( x ( 0 ) ), (7.16)
де k = 0, 1, 2, … .
На підставі (7.16) одержимо: рівняння (7.16) задовольняється у
загальному випадку і для обернених матриць, тобто,

W − 1 ( x  ( k ) ) = W − 1 ( x ( 0 ) ). (7.17)

63