Page 59 - 6769

Запам’ятайте: чим ближче Ви до значення коренів (чим
менше значення ), тим з меншим приростом треба змінювати
струми.

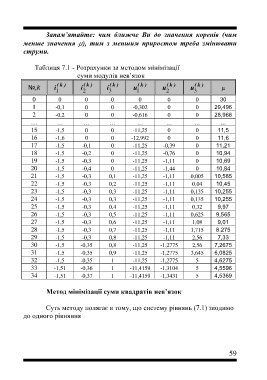
Таблиця 7.1 - Розрахунки за методом мінімізації
суми модулів нев’язок
№,k i 1 ( k ) i ( 2 k ) i 3 ( k ) u 1 ( k ) u 2 ( k ) u 3 ( k ) 

0 0 0 0 0 0 0 30
1 -0,1 0 0 -0,302 0 0 29,496
2 -0,2 0 0 -0,616 0 0 28,968
… … … … … … … …
15 -1,5 0 0 -11,25 0 0 11,5
16 -1,6 0 0 -12,992 0 0 11,6
17 -1,5 -0,1 0 -11,25 -0,39 0 11,21
18 -1,5 -0,2 0 -11,25 -0,76 0 10,94
19 -1,5 -0,3 0 -11,25 -1,11 0 10,69
20 -1,5 -0,4 0 -11,25 -1,44 0 10,84
21 -1,5 -0,3 0,1 -11,25 -1,11 0,005 10,585
22 -1,5 -0,3 0,2 -11,25 -1,11 0,04 10,45
23 -1,5 -0,3 0,3 -11,25 -1,11 0,135 10,255
24 -1,5 -0,3 0,3 -11,25 -1,11 0,135 10,255
25 -1,5 -0,3 0,4 -11,25 -1,11 0,32 9,97
26 -1,5 -0,3 0,5 -11,25 -1,11 0,625 9,565
27 -1,5 -0,3 0,6 -11,25 -1,11 1,08 9,01
28 -1,5 -0,3 0,7 -11,25 -1,11 1,715 8,275
29 -1,5 -0,3 0,8 -11,25 -1,11 2,56 7,33
30 -1,5 -0,35 0,8 -11,25 -1,2775 2,56 7,2675
31 -1,5 -0,35 0,9 -11,25 -1,2775 3,645 6,0825
32 -1,5 -0,35 1 -11,25 -1,2775 5 4,6275
33 -1,51 -0,36 1 -11,4159 -1,3104 5 4,5596
34 -1,51 -0,37 1 -11,4159 -1,3431 5 4,5369

Метод мінімізації суми квадратів нев’язок

Суть методу полягає в тому, що систему рівнянь (7.1) зводимо
до одного рівняння

59