Page 51 - 6769

(k)
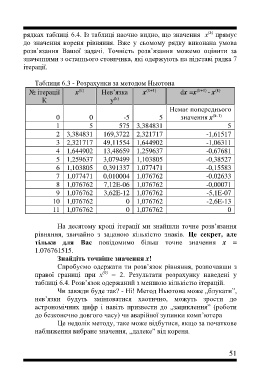
рядках таблиці 6.4. Із таблиці наочно видно, що значення х прямує
до значення кореня рівняння. Вже у сьомому рядку виконана умова
розв’язання Вашої задачі. Точність розв’язання можемо оцінити за
значеннями з останнього стовпчика, які одержують на підставі рядка 7
ітерації.

Таблиця 6.3 - Розрахунки за методом Ньютона
(k)
(k)
№ ітерації x Нев’язка x (k+1) dx =x (k+1) - x
(k)
К y
Немає попереднього
0 0 -5 5 значення x (k-1)
1 5 575 3,384831 5
2 3,384831 169,3722 2,321717 -1,61517
3 2,321717 49,11554 1,644902 -1,06311
4 1,644902 13,48659 1,259637 -0,67681
5 1,259637 3,079499 1,103805 -0,38527
6 1,103805 0,391337 1,077471 -0,15583
7 1,077471 0,010004 1,076762 -0,02633
8 1,076762 7,12E-06 1,076762 -0,00071
9 1,076762 3,62E-12 1,076762 -5,1E-07
10 1,076762 0 1,076762 -2,6E-13
11 1,076762 0 1,076762 0

На десятому кроці ітерації ми знайшли точне розв’язання
рівняння, звичайно з заданою кількістю знаків. Це секрет, але
тільки для Вас повідомимо більш точне значення x =
1.076761515.
Знайдіть точніше значення x!
Спробуємо одержати ти розв’язок рівняння, розпочавши з
(0)
правої границі при х = 2. Результати розрахунку наведені у
таблиці 6.4. Розв’язок одержаний з меншою кількістю ітерацій.
Чи завжди буде так? - Ні! Метод Ньютона може „блукати”,
нев’язки будуть змінюватися хаотично, можуть зрости до
астрономічних цифр і навіть призвести до „зациклення” (роботи
до безконечно довгого часу) чи аварійної зупинки комп’ютера
Це недолік методу, таке може відбутися, якщо за початкове
наближення вибране значення, „далеке” від кореня.

51