Page 48 - 6769

коли x = 0,294118 ,(нев’язка y1(0,294118) = -4,751679, x = , 2
2
1
(нев’язка y2(2) = 29).
За формулою (4.5) знаходимо

(2)
x = 0,294118 – (-4,751679)(2-0,294118)/(29 – (-4,751679)) =
0,534278.

(2)
На підставі значення x знайдемо значення нев’язки
2
3
(2)
y = 5(0,534278) -2(0,534278) + 0,534278 -4,751679 = -4,274073.
Уважно розглядаючи рядки 1 та 2 таблиці 4.1, Ви там знайдете
результати обчислень, які одержано у 1 та 2 ітераціях.
Швидкість наближення до кореня рівняння (див. стовпчик x1)
(k)
сповільнюється. Нев’язка y прямує до нуля.
У методі хорд інколи важко оцінити точність знайденого
кореня, це можна інтуїтивно відчувати, якщо припустити , що ми
наблизилися до значення кореня, коли величина x мала. Однак,
трапляються випадки, коли x мале, а ми знаходимося „далеко” від
кореня рівняння.
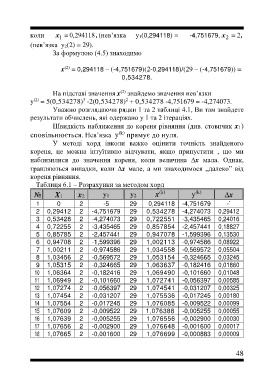
Таблиця 6.1 – Розрахунки за методом хорд
(k)
(k)
№ X1 x2 y1 y2 x y x
1 0 2 -5 29 0,294118 -4,751679 -`
2 0,29412 2 -4,751679 29 0,534278 -4,274073 0,29412
3 0,53428 2 -4,274073 29 0,722551 -3,435465 0,24016
4 0,72255 2 -3,435465 29 0,857854 -2,457441 0,18827
5 0,85785 2 -2,457441 29 0,947078 -1,599396 0,13530
6 0,94708 2 -1,599396 29 1,002113 -0,974586 0,08922
7 1,00211 2 -0,974586 29 1,034558 -0,569572 0,05504
8 1,03456 2 -0,569572 29 1,053154 -0,324665 0,03245
9 1,05315 2 -0,324665 29 1,063637 -0,182416 0,01860
10 1,06364 2 -0,182416 29 1,069490 -0,101660 0,01048
11 1,06949 2 -0,101660 29 1,072741 -0,056397 0,00585
12 1,07274 2 -0,056397 29 1,074541 -0,031207 0,00325
13 1,07454 2 -0,031207 29 1,075536 -0,017245 0,00180
14 1,07554 2 -0,017245 29 1,076085 -0,009522 0,00099
15 1,07609 2 -0,009522 29 1,076388 -0,005255 0,00055
16 1,07639 2 -0,005255 29 1,076556 -0,002900 0,00030
17 1,07656 2 -0,002900 29 1,076648 -0,001600 0,00017
18 1,07665 2 -0,001600 29 1,076699 -0,000883 0,00009

48