Page 33 - 6639

Розв’язок.

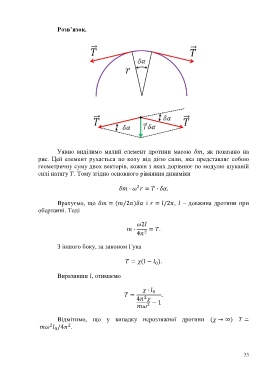
Уявно виділимо малий елемент дротини масою , як показано на
рис. Цей елемент рухається по колу під дією сили, яка представляє собою
геометричну суму двох векторів, кожен з яких дорівнює по модулю шуканій
силі натягу . Тому згідно основного рівняння динаміки

∙ = ∙ .

Врахуємо, що = ( /2 ) і = /2 , – довжина дротини при
обертанні. Тоді

2
∙ = .
4

З іншого боку, за законом Гука

= ( − ).

Виразивши , отимаємо

 ∙
= .

4  − 1

Відмітимо, що у випадку нерозтяжної дротини ( → ∞) =

/4 .

33