Page 16 - 6378

Частинка в ямі довільної форми не може знаходитися на її дні, оскільки в нуль

перетворюється імпульс частинки і його невизначеність, а невизначеність координати стає
нескінченною, що протирічить, в свою чергу, умові перебування частинки в потенціальній

ямі.

Правилами відбору у квантовій механіці називають умови, які накладаються на
зміну квантових чисел.

Для гармонічного осцилятора можливі тільки переходи між сусідніми підрівнями,

тобто переходи, які задовільняють правилу відбору:

∆ = ±1.

Отже, енергія гармонічного осцилятора може змінюватися тільки порціями ℏ і
гармонічний осцилятор випромінює і поглинає енергію квантами.

Квантово-механічний розв’язок задачі про квантовий осцилятор показує, що є

відмінна від нуля ймовірність виявити частинку за межами області − ≤ ≤ + .
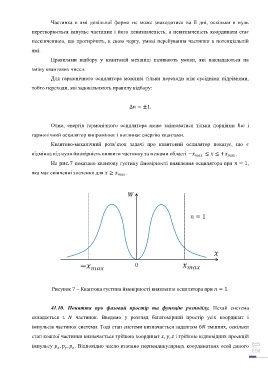
На рис. 7 показано квантову густину ймовірності виявлення осцилятора при = 1,

яка має скінченні значення для ≥ .

Рисунок 7 – Квантова густина ймовірності виявлення осцилятора при = 1.

41.10. Поняття про фазовий простір та функцію розподілу. Нехай система

складається з частинок. Введемо у розгляд багатомірний простір усіх координат і

імпульсів частинок системи. Тоді стан системи визначається заданням 6 змінних, оскільки
стан кожної частинки визначається трійкою координат , , і трійкою відповідних проекцій

імпульсу , , . Відповідно число взаємно перпендикулярних координатних осей даного