Page 14 - 6378

2
2
Тут = 2 , = 2(−) .
ℏ 2 ℏ 2
Таким чином, квантова механіка приводить до принципово нового специфічного
квантового явища, яке отримало назву тунельного ефекту, в результаті якого мікрооб’єкт

може пройти через потенціальний бар’єр.

Для опису тунельного ефекту використовують поняття коефіцієнта прозорості
потенціального бар’єру, який визначається як відношення квадратів модулів хвилі, яка

пройшла бар’єр і падає на нього:

2 2
3
= = exp − 2( − ) . (21)
2 0 ℏ
1

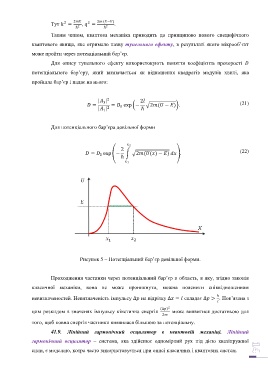
Для потенціального бар’єра довільної форми

2
2
= exp − 2(() − ) . (22)
0
ℏ
1

Рисунок 5 – Потенціальний бар’єр довільної форми.

Проходження частинки через потенціальний бар’єр в область, в яку, згідно законів

класичної механіки, вона не може проникнути, можна пояснити співвідношенням

невизначеностей. Невизначеність імпульсу ∆ на відрізку ∆ = складає ∆ > . Пов’язана з

цим розкидом в значенях імпульсу кінетична енергія ∆ 2 може виявитися достатньою для
2
того, щоб повна енергія частинки виявилася більшою за потенціальну.

41.9. Лінійний гармонічний осцилятор в квантовій механіці. Лінійний

гармонічний осцилятор – система, яка здійснює одномірний рух під дією квазіпружної
сили, є моделлю, котра часто використовується при описі класичних і квантових систем.