Page 15 - 6378

Пружинний, фізичний та математичний маятники – приклади класичних

гармонічних осциляторів.
2 2

0
Потенціальна енергія гармонічного осцилятора дорівнює: = , де – власна
0
2
частота коливань осцилятора; – маса частинки.
Класичний осцилятор не може вийти за межі потенціальної ями з координатами

− ≤ ≤ + .
Рівняння Шредінгера для стаціонарних станів квантового осцилятора:

2 2
2
2
+ − 0 = 0, (23)
2 ℏ 2 2

де – повна енергія осцилятора.
Власні значення енергії для цього рівняння:

1
= + ℏ = 0, 1, 2, … . (24)

2 0

Таким чином, енергія квантового осцилятора квантується (може мати тільки
дискретні значення). Рівні енергії розміщені на однакових відстанях, рівних ℏ .
0

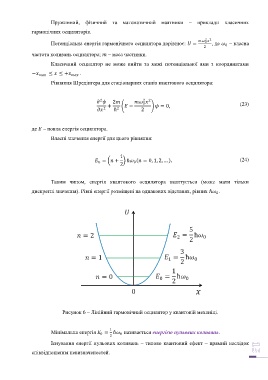
Рисунок 6 – Лінійний гармонічний осцилятор у квантовій механіці.

1
Мінімальна енергія = ℏ називається енергією нульових коливань.
0
0
2
Існування енергії нульових коливань – типово квантовий ефект – прямий наслідок
співвідношення невизначеностей.