Page 122 - 5637

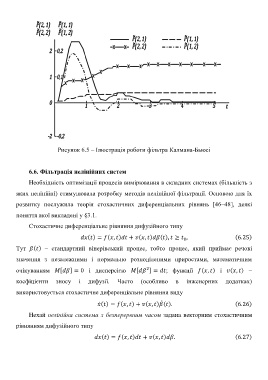
Рисунок 6.5 – Ілюстрація роботи фільтра Калмана-Бьюсі

6.6. Фільтрація нелінійних систем

Необхідність оптимізації процесів вимірювання в складних системах (більшість з

яких нелінійні) стимулювала розробку методів нелінійної фільтрації. Основою для їх

розвитку послужила теорія стохастичних диференціальних рівнянь [46–48], деякі

поняття якої викладені у §3.1.

Стохастичне диференціальне рівняння дифузійного типу

( ) = ( , ) + ( , ) ( ), ≥ , (6.25)

Тут ( ) – стандартний вінерівський процес, тобто процес, який приймає речові

значення з незалежними і нормально розподіленими приростами, математичним

очікуванням [ ] = 0 і дисперсією [ ] = ; функції ( , ) і ( , ) –
коефіцієнти зносу і дифузії. Часто (особливо в інженерних додатках)

використовується стохастичне диференціальне рівняння виду

̇
̇( ) = ( , ) + ( , ) ( ). (6.26)
Нехай нелінійна система з безперервним часом задана векторним стохастичним

рівнянням дифузійного типу

( ) = ( , ) + ( , ) . (6.27)