Page 109 - 5637

де – масив поточного вектора вхідного сигналу; – вихідний сигнал системи;

– розмірність масиву ХК; – формування скалярного твори для обчислення

вихідного сигналу.

Приклад. Ідентифікація системи, вхід і вихід якої описуються рівняннями

= + ,

де [ , ] – двовимірний масив вектора вхідних сигналів; - скалярний вихідний

сигнал; [ , ] – двовимірний масив вектора параметрів системи, що підлягає

ідентифікації: = 2, = 3. Величини і – незалежні гаусові стаціонарні

процеси з математичним очікуванням і кореляційної функцією кожного процесу

( ) = exp{− | |} (тут , > 0 – константи).

Величини ( = 1, 2) моделювалися за допомогою наступних рекурентних

співвідношень [44]:

∆ ( ) = 2√12 [ ( ) − 0,5]√ ∆ ,

∆ ( ) = − [ ( ) − ∆ ( )],

( ) = ( − 1) + ∆ ( )∆ ,

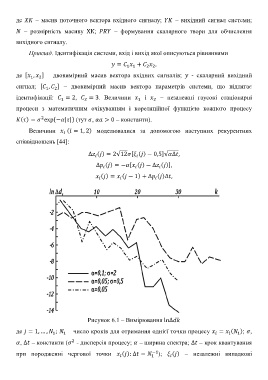
Рисунок 6.1 – Вимірювання ln∆

де = 1, … , ; – число кроків для отримання однієї точки процесу = ( ); ,

, ∆ – константи ( - дисперсія процесу; – ширина спектра; ∆ – крок квантування
при породженні чергової точки ( ): ∆ = ); ( ) – незалежні випадкові