Page 29 - 4974

f  z f  z f  z f  0 f  0 f  0
1 2 5 1 2 5
  f  m f  m f  ,m   f  m f  m f  ,m
1 2 5 1 1 2 5
f 1  n f 2  n f 5  n f 1  n f 2  n f 5  n

f  0 f  0 f  0 f  0 f  0 f  0
1 2 5 1 2 5
  f  z f  z f   ,z   f  m f  m f  ,m
n 1 2 5 m 1 2 5
f 1  n f 2  n f 5  n f 1  z f 2  z f 5  z

а сталі коефіцієнти
1 1
a  , b  .
f 3  0 f 4  0

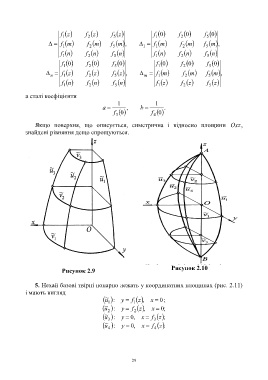
Якщо поверхня, що описується, симетрична і відносно площини Oxz,
знайдені рівняння дещо спрощуються.

Рисунок 2.10
Рисунок 2.9

5. Нехай базові твірні попарно лежать у координатних площинах (рис. 2.11)
і мають вигляд
~
 : yu 1  f 1  ,z x  0 ;
~
 : yu 2  f 2  ,z x  ; 0
~
 : yu 3  , 0 x  f 3  ;z
~
 : yu 4  , 0 x  f 4  .z

29