Page 32 - 4974

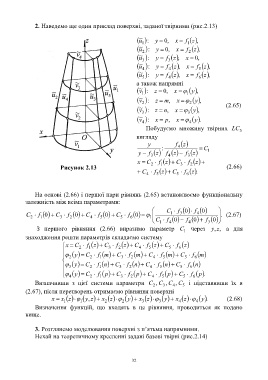
2. Наведемо ще один приклад поверхні, заданої твірними (рис.2.13)

~
 : yu  , 0 x  f  ,z
1 1
~
 : yu 2  , 0 x  f 2  ,z
~
 : yu 3  f 3  ,z x  , 0
~
 : yu 4  f 4  ,z x  f 5  ,z
~
 : yu  f  ,z x  f  ,z
5 4 6
а також напрямні
~
 : zv 1  , 0 x  1  ,y
~
 : zv 2  , m x  2  ,y
~ (2.65)
 : zv  , n x   ,y
3 3
~
 : xv 4  , p x  4  .y
Побудуємо множину твірних LC
5
вигляду
y f  z
: 4  C
1
y  f 3   fz 4  z  f 3  z
x  C 2 f  1   Cz  3 f  2   z 
Рисунок 2.13 (2.66)
 C 4 f  5   Cz  5 f  6  .z

На основі (2.66) і першої пари рівнянь (2.65) встановлюємо функціональну
залежність між всіма параметрами:

 C  f   0  f   0 
C  f  0  C  f  0  C  f  0  C  f  0   1 3 4 .  (2.67)
2 1 3 2 4 5 5 6 1 
 C 1  f 4  0  f 4  0  f 3  0 
З першого рівняння (2.66) виразимо параметр C через y , , z а для
1
знаходження решти параметрів складаємо систему
  Cx 2  f 1   Cz 3  f 2   Cz 4  f 5    Cz 5  f 6  z


 2    Cy 2  f 1    Cm 3  f 2   Cm 4  f 5   Cm 5  f 6  m


 3   Cy 2  f 1    Cn 3  f 2   Cn 4  f 5    Cn 5  f 6  n
     Cy  f   Cp  f   Cp  f    Cp  f  .p
 4 2 1 3 2 4 5 5 6
Визначивши з цієї системи параметри C , C , C , C і підставивши їх в
2 3 4 5
(2.67), після перетворень отримаємо рівняння поверхні
x  x  z   ,zy  x  z    xy   z    xy   z   .y (2.68)
1 1 2 2 3 3 4 4
Визначення функцій, що входять в це рівняння, проводиться як подано
вище.

3. Розглянемо моделювання поверхні з п’ятьма напрямними.
Нехай на теоретичному кресленні задані базові твірні (рис.2.14)

32