Page 14 - 4974

y  y
1  . C (1.43)
y  y
2 1
Із цієї властивості випливають дві інші.

Властивість 2. Січні до інтегральних кривих лінійного рівняння, проведені
через точки перетину цих кривих двома будь-якими прямими, паралельними до
осі Oy , перетинаються в одній і тій самій точці або паралельні (рис. 1.3).
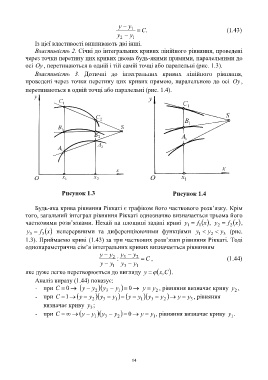
Властивість 3. Дотичні до інтегральних кривих лінійного рівняння,
проведені через точки перетину цих кривих прямою, паралельною до осі Oy ,
перетинаються в одній точці або паралельні (рис. 1.4).

Рисунок 1.3 Рисунок 1.4

Будь-яка крива рівняння Ріккаті є графіком його часткового розв’язку. Крім
того, загальний інтеграл рівняння Ріккаті однозначно визначається трьома його
частковими розв’язками. Нехай на площині задані криві y  f 1  x , y  f 2  x ,
2
1
y  f  x неперервними та диференціюючими функціями y  y  y (рис.
3 3 1 2 3
1.3). Приймаємо криві (1.43) за три часткових розв’язки рівняння Ріккаті. Тоді
однопараметрична сім’я інтегральних кривих визначається рівнянням
y  y y  y
2 : 3 2  C , (1.44)
y  y y  y
1 3 1
яке дуже легко перетворюється до вигляду y   Cx, .
Аналіз виразу (1.44) показує:
- при C  0    yy 2 y 3  y 1  0  y  y , рівняння визначає криву y ,
2
2
- при C  1 y  y 2 y  y 1  y  y 1 y  y 2  y  y , рівняння
3
3
3
визначає криву y ;
3
- при C    y  y 1 y  y 2  0  y  y , рівняння визначає криву y .
1
3
1

14