Page 65 - 4845

8 9 7 11
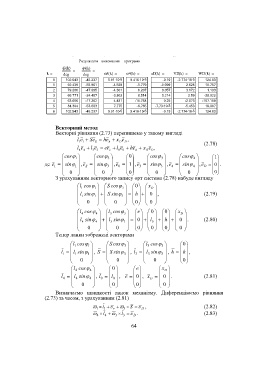
Результати виконання програми
3k()  4k() 
k  deg deg  3k()   4k()  xD k()  VD k()  WD k() 
0 102.543 -45.237 5.91·10 -5 9.416·10 -5 -0.19 -2.774·10 -5 124.03
1 92.439 -55.961 -4.529 -1.779 -0.099 2.628 18.757
2 79.206 -47.895 -4.301 6.207 0.057 3.172 1.193
3 66.771 -24.487 -3.802 8.514 0.214 2.59 -28.022
4 63.656 -17.262 4.481 -10.758 0.25 -2.873 -157.159
5 84.304 -53.883 7.775 -6.765 -7.73·10 -3 -5.453 19.807
6 102.543 -45.237 5.91·10 -5 9.416·10 -5 -0.19 -2.774·10 -5 124.03

Векторний метод
Векторні рівняння (2.73) перепишемо у такому вигляді
l e  e S  e h  x e ,
1 1 S h D D (2.78)
l 4 e  l 3 e  e e e  l 0 e  e h h  x D e D ,
0
3
4
cos  1  cos  3      0  cos  3  cos  4    1












де e 1  sin  1  ,e S  sin  3  ,e 0  1 ,e 3  sin  3  ,e 4  sin  4  , e D      0 .

 0    0     0   0   0    0  







З урахуванням векторного запису орт система (2.78) набуде вигляду
 cosl 1  1   cosS  3    0   x D  






l
 1 sin 1   S sin 3   h   0 , (2.79)




       
 0   0   0   0 
 cosl 4  4   cosl 3  3    e   0      0   x D  







 4 sin 4   l sin 3   0   l   h    0 . (2.80)
l



 0
 3
           
 0   0   0   0   0   0 
Тепер ланки зображені векторами
 cosl 1  1    cosS  3    cosl 3  3     0 




l 1  l sin  1  , S  S sin  3  , l 3  l sin  3  , h  h ,



 1
 3
       
 0   0   0   0 
 cosl 4  4   0      e   x D 








l 4  l sin  4  , l 0  l  , e  0 , x D   0 . (2.81)
 4
 0
       
 0   0   0   0 
Визначаємо швидкості ланок механізму. Диференціюємо рівняння
(2.73) за часом, з урахуванням (2.81)
  l      S   , (2.82)
r
3
D
1
1
  l    l   . (2.83)
3
4
4
D
3
64