Page 98 - 4754

96

l : 12 x  10 y  15  0 – пряма лінія. ■

7.2. Рівняння прямої з кутовим коефіцієнтом

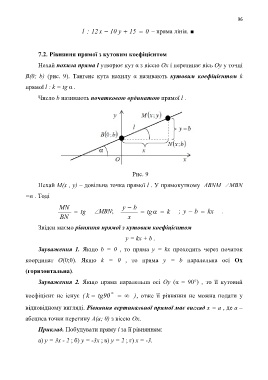
Нехай похила пряма l утворює кут α з віссю Ox і перетинає вісь Oy у точці

B(0; b) (рис. 9). Тангенс кута нахилу α називають кутовим коефіцієнтом k

прямої l : k = tg α .

Число b називають початковою ординатою прямої l .

Рис. 9

Нехай M(x , y) – довільна точка прямої l . У прямокутному ΔBNM MBN

=α . Тоді

MN y  b
 tg MBN;  tg  k ; y  b  kx .
BN x

Звідси маємо рівняння прямої з кутовим коефіцієнтом

y = kx + b .

Зауваження 1. Якщо b = 0 , то пряма y = kx проходить через початок

координат O(0;0). Якщо k = 0 , то пряма y = b паралельна осі Ox

(горизонтальна).

Зауваження 2. Якщо пряма паралельна осі Oy (α = 90°) , то її кутовий


коефіцієнт не існує k(  tg90   ) , отже її рівняння не можна подати у

відповідному вигляді. Рівняння вертикальної прямої має вигляд x = a , де a –

абсциса точки перетину A(a; 0) з віссю Ox.

Приклад. Побудувати пряму l за її рівнянням:

а) y = 3x - 2 ; б) y = -3x ; в) y = 2 ; г) x = -3.