Page 17 - 4744

c) f   0c – коренем рівняння є x  .
c
При цьому будується стискуюче відображення інтервалу  ba; , яке
реалізується у вигляді послідовності вкладених відрізків, які, за
відомою лемою, мають єдину спільну точку, яка і буде коренем

рівняння.
У методі хибного положення на інтервалі, на кінцях якого

функція приймає значення різних знаків, а перша і друга похідні
зберігають знак, будується січна (рисунок 1.1), що проходить
через точки з координатами a, f  a ,  fb,  b , після чого знаходяться

координати точки перетину січної  0;c , і знаходиться точка

 fc,  c . Будується нова січна. Вказаний процес повторюється до
тих пір, поки не буде знайдено розв’язок – точка R . Зауважимо,
що ненульова координата точки  0;c визначається за формулою:
b  a
c  a  f  a  (1.5)
f  b  f  a

.
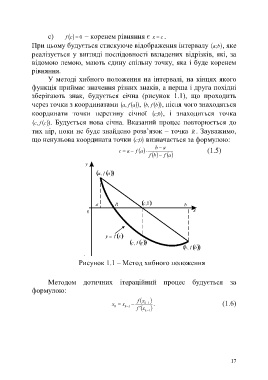
Рисунок 1.1 – Метод хибного положення

Методом дотичних ітераційний процес будується за

формулою:

f x 
x  x  k  1 . (1.6)
k k  1
f   x 
k  1

17