Page 21 - 4621

Якщо  pX  1 p є одиничною функцією, то перехідна функція коливальної
ланки набуває вигляду:

  1  
h    kt  1  e  Tt cos  t 0 sin  T 0  , (3.34)



   0 T  

2T 4T  T 2
де T  1 ,   1 2 .
T 2T
2 1
Схематичний вигляд перехідної характеристики коливальної ланки наведено на
рис. 3.8.

y
2 T  T
1
2
x

x  t y  t
1
2 T  T
1
2

0 t 0 t

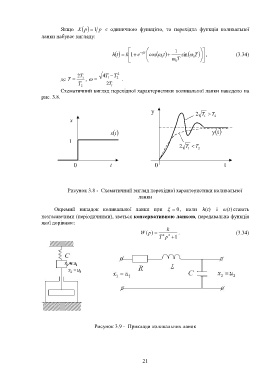
Рисунок 3.8 - Схематичний вигляд перехідної характеристики коливальної
ланки

Окремий випадок коливальної ланки при   0 , коли h (t ) і  (t )стають
незгасаючими (періодичними), зветься консервативною ланкою, передавальна функція
якої дорівнює:
k
W (p )  . (3.34)
T 2 p 2  1

Рисунок 3.9 - Приклади коливальних ланок

21