Page 25 - 4621

Аналітичний вираз для логарифмічної амплітудно-частотної характеристики
має вигляд:

 k  2 2
j
L  lg k    lg   lg k  lg 1 T  L  L . (4.4)
1
2
2
1   2 T 

ЛАЧХ складається з двох доданків і наближено може бути поданий ламаною
лінією. Таку наближену характеристику називають асимптотичною логарифмічною
амплітудно-частотною характеристикою.
При   1 T у виразі (4.4) можна знехтувати другим доданком. Тоді
k
асимптотична ЛАЧХ є прямою, паралельною до осі абсцис з ординатою lg при
  0 .
При  1 T можна знехтувати першим доданком. У цьому разі асимптотична
ЛАЧХ є прямою, що описується рівнянням

2
L  lg k lg 1  2 T  lg k lg  T . (4.5)

Ця лінія є другою асимптотою, до якої прямує ЛАЧХ при    . Обидві
асимптоти перетинаються в точці   1 T . Цю частоту називають спрягаючою.
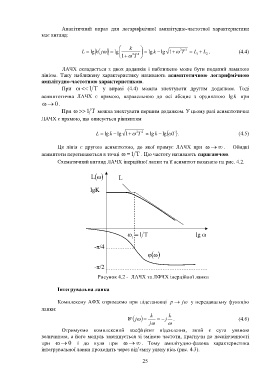
Схематичний вигляд ЛАЧХ інерційної ланки та її асимптот показано на рис. 4.2.

L   L

lgK

  1 T lg ω
1

-π/4
  

-π/2

Рисунок 4.2 - ЛАЧХ та ЛФЧХ інерційної ланки

Інтегрувальна ланка

Комплексну АФХ отримаємо при підстановці p   j у передавальну функцію
ланки:
k k
W  j    j . (4.6)
 j 
Отримуємо комплексний коефіцієнт підсилення, який є суто уявною
величиною, а його модуль зменшується зі зміною частоти, прагнучи до нескінченності
при   0 і до нуля при    . Тому амплітудно-фазова характеристика
інтегрувальної ланки проходить через від’ємну уявну вісь (рис. 4.3).

25