Page 31 - 4443

Обчислення потрійного інтеграла

t
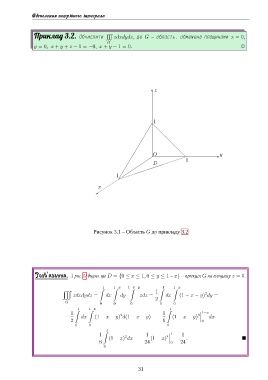
Приклад 3.2. Обчислити zdxdydz, де G — область, обмежена площинами x = 0,
G
y = 0, x + y + z − 1 = −0, x + y − 1 = 0. ,

z
6

1
@
@
@
@
@
@
O @

@ - y
D 1

1

x

+

Рисунок 3.1 – Область G до прикладу 3.2

Розв’язання. З рис. 3.1 видно, що D = {0 ≤ x ≤ 1, 0 ≤ y ≤ 1−x} — проекція G на площину z = 0.

1 1−x 1−x−y 1 1−x
∫ ∫ ∫ ∫ ∫
y 1
2
zdxdydz = dx dy zdz = dx (1 − x − y) dy =
2
G
0 0 0 0 0
1 1−x 1
∫ ∫ ∫
1 2 1 1−x
3
= − dx (1 − x − y) d(1 − x − y) = − (1 − x − y) dx =
2 6 0
0 0 0
1
∫
1 1 1 1
3
4
= (1 − x) dx = − (1 − x) = .
6 24 0 24
0
31