Page 23 - 4443

Застосування подвійних інтегралів до задач геометрії

Отже,
√
2
2
∆σ i = (f (ξ i , η i )) + (f (ξ i , η i )) + 1∆S i .
′
′
x
y
Підставляючи значення ∆σ i в (2.11), дістаємо
n √
∑
2
Q = lim (f (ξ i , η i )) + (f (ξ i , η i )) + 1∆S i .
2
′
′
λ→0 x y
i=1
Під знаком границі маємо інтегральну суму, побудовану для неперервної в області D фун-
√
кції (f (x, y)) + (f (x, y)) + 1. Ця функція інтегровна в області D, тому границя у
2
2
′
′
x
y
формулі (2.11) існує і дорівнює подвійному інтегралу (2.9).
2
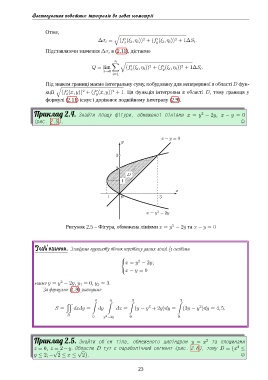
Приклад 2.4. Знайти площу фігури, обмеженої лініями x = y − 2y, x − y = 0
(рис. 2.5). ,
x − y = 0
y
3

2
D
1
x
−1 0 3

2
x = y − 2y

2
Рисунок 2.5 – Фігура, обмежена лініями x = y − 2y та x − y = 0

Розв’язання. Знайдемо ординату точок перетину даних ліній. Із системи

{
2
x = y − 2y;
x − y = 0

2
маємо y = y − 2y, y 1 = 0, y 2 = 3.
За формулою (1.9) знаходимо

3 y 3 3
x ∫ ∫ ∫ ∫
2
2
S = dxdy = dy dx = (y − y + 2y)dy = (3y − y )dy = 4, 5.
D 0 y −2y 0 0
2

Приклад 2.5. Знайти об’єм тіла, обмеженого циліндром y = x 2 та площинами
2
z = 0, z = 2 − y. Областю D тут є параболічний сегмент (рис. 2.6), тому D = {x ≤
√ √
y ≤ 2; − 2 ≤ x ≤ 2}. ,

23