Page 120 - 4443

Ряди Фур’є

y

f(x)

x
. . . . . . .
−l 0 l

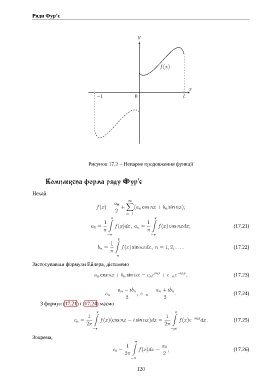
Рисунок 17.2 – Непарне продовження функції

Комплексна форма ряду Фур’є

Нехай

∞
∑
a 0
f(x) = + (a n cos nx + b n sin nx);
2
n=1
π π
∫ ∫
1 1
a 0 = f(x)dx, a n = f(x) cos nxdx; (17.21)
π π
−π −π
π
∫
1
b n = f(x) sin nxdx, n = 1, 2, . . . . (17.22)
π
−π
Застосувавши формули Ейлера, дістанемо
a n cos nx + b n sin nx = c n e inx + c −n e −inx , (17.23)

a n − ib n a n + ib n
c n = , c −n = . (17.24)
2 2
З формул (17.21) і (17.24) маємо
π π
∫ ∫
1 1
c n = f(x)(cos nx − i sin nx)dx = f(x)e −inx dx. (17.25)
2π 2π
−π −pi
Зокрема,
π
∫
1 a 0
c 0 = f(x)dx = , (17.26)
2π 2
−π

120