Page 119 - 4443

Ряди Фур’є для функцій заданих на відрізку [0;l] або на відрізку [a;b]

y

f(x)

x
. . . . . . .
−l 0 l

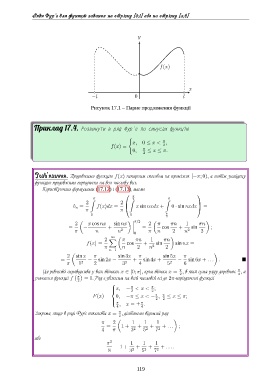
Рисунок 17.1 – Парне продовження функції

Приклад 17.4. Розвинути в ряд Фур’є по синусах функцію

{
π
x, 0 ≤ x < ,
f(x) = 2
0, π ≤ x ≤ π.
2

Розв’язання. Продовжимо функцію f(x) непарним способом на проміжок [−π; 0), а потім знайдену
функцію продовжимо періодично на всю числову вісь.
Користуючись формулами (17.12) і (17.13), маємо
 π 
π π
∫ 2 ∫ ∫
2 2 

b n = f(x)dx =  x sin nxdx + 0 · sin nxdx =
π π
0 0 π
2
( ) π/2 ( )
2 x cos nx sin nx 2 π πn 1 πn
= − + = cos + sin ;
π n n 2 π n 2 n 2 2
0
∞ ( )
2 ∑ π πn 1 πn
f(x) = cos + sin sin nx =
π n 2 n 2 2
n=1
( )
2 sin x π sin 3x π sin 5x π
= − sin 2x − + sin 4x + − sin 6x + . . . .
π 1 2 2 3 2 4 5 2 6
Ця рівність справедлива у всіх точках x ∈ [0; π], крім точки x = , в якій сума ряду дорівнює , а
π
π
( ) 2 4
значення функції f π = 0. Ряд є збіжним на всій числовій осі до 2π-періодичної функції
2

π
π
x, − < x < ;
 2 2
π
F(x) = 0, −π ≤ x < − , π ≤ x ≤ π;
2 2

π
 π , x = ± .
4 4
π
Зокрема, якщо в ряді Фур’є покласти x = , дістанемо відомий ряд
2
( )
π 2 1 1 1
= 1 + + + + . . . ;
4 π 3 2 5 2 7 2
або
π 2 1 1 1
= 1 + + + + . . . .
8 3 2 5 2 7 2
119