Page 184 - 4371

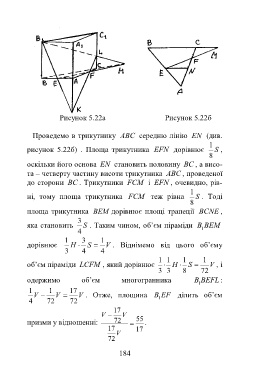
Рисунок 5.22а Рисунок 5.22б

Проведемо в трикутнику ABC середню лінію EN (див.
1
рисунок 5.22б) . Площа трикутника EFN дорівнює S ,
8
оскільки його основа EN становить половину BC , а висо-
та – четверту частину висоти трикутника ABC , проведеної
до сторони BC . Трикутники FCM і EFN , очевидно, рів-
1
ні, тому площа трикутника FCM теж рівна S . Тоді
8
площа трикутника BEM дорівнює площі трапеції BCNE ,
3
яка становить S . Таким чином, об’єм піраміди B 1 BEM
4
1 3 1
дорівнює H  S  V . Віднімемо від цього об’єму
3 4 4
1 1 1 1
об’єм піраміди LCFM , який дорівнює  H  S  V , і
3 3 8 72
одержимо об’єм многогранника B BEFL :
1
1 1 17
V  V  V . Отже, площина B 1 EF ділить об’єм
4 72 72
17
V  V
призми у відношенні: 72  55 .
17 17
V
72
184