Page 73 - 4204

ЛЕКЦІЯ 6. ПРОСТОРОВА ІНТЕРПОЛЯЦІЯ. ПОБУДОВА ЦИФРОВИХ МОДЕЛЕЙ РЕЛЬЄФУ

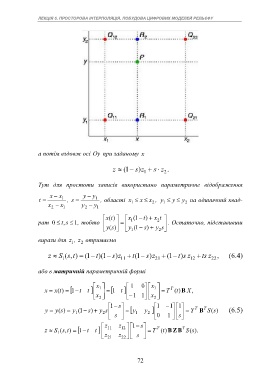
а потім вздовж осі Oy при заданому x

z  1 (  s )z  s z  2 .
1

Тут для простоти записів використано параметричне відображення

x  x y  y
t  1 , s  1 , області x  x  x , y  y  y на одиничний квад-
x  x y  y 1 2 1 2
2 1 2 1

 tx(  ) x 1(  t)  x 2 t 
1
рат 0  t , s 1, тобто      . Остаточно, підставивши
y 1(
 y( s)   1  s)  y 2 s 
вирази для z , z отримаємо
1 2

z  S 1 (s ,t )  1 ( )( t  1 s )z  1 ( t  s )z  1 (  t ) zs 12  ts z , (6.4)
22
11
21
або в матричній параметричній формі

 x   1 0   x 
x  x (t )   1 t  t  1    1 t     1   T T (t )B X ,
 x 2   1 1   x 2
  1   1  1
1 s
T

s
y  y (s )  y 1 1 (  ) s  y 2    y 1 y 2      Y B T S (s ) (6.5)
 s   0 1   s 
1 s
z  z   
z  S (s ,t )   1 t  t 11 12  T T (t ) ZB B T S (s ).
1    
 z 21 z 22   s 

72