Page 45 - 4204

ЛЕКЦІЯ 4. ІНТЕРПОЛЯЦІЯ СПЛАЙНАМИ

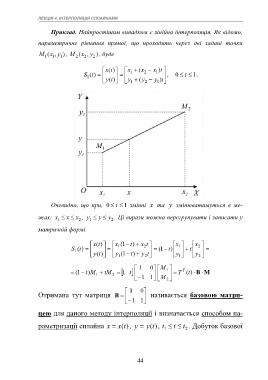
Приклад. Найпростішим випадком є лінійна інтерполяція. Як відомо,

параметричне рівняння прямої, що проходить через дві задані точки

M (x , y ), M (x , y ), буде
1 1 1 2 2 2

 tx(  ) x  x(  x  t )
S ( t)      1 2 1  , 0  t  1.
1
y
 y( t)   1  y( 2  y ) t 
1

M
2

M 1

Очевидно, що при, 0  t  1 змінні x та y змінюватимуться в ме-

жах: x  x  x , y  y  y . Ці вирази можна перегрупувати і записати у
1
2
1
2
матричній формі
 (tx  )  (x 1 1  )t  x 2  t x 1  x 2 
S (t )    1(  )t  t 
1        
y
y
y
 y (t )   1 1 (  )t  y 2 t   1   2 
 1  0 M 
 1(  )Mt 1  tM 2   1 t    1   T T (t  ) B  M
 1 1   M 2 

 1  0
Отримана тут матриця B    називається базовою матри-
 1 1 

цею для даного методу інтерполяції і визначається способом па-

раметризації сплайна x  x (t ), y  y ) (t , t  t  t . Добуток базової
1 2

44