Page 39 - 4204

ЛЕКЦІЯ 4. ІНТЕРПОЛЯЦІЯ СПЛАЙНАМИ

терполяцію. Сплайни також застосовуються в автоматичному ка-

ртографуванні для побудови цифрових моделей рельєфу.

4.1. Означання сплайн-функції

Нехай відрізок [a , ] b розбитий на n відрізків [x i , x  i 1 ], точ-

a
ками x , i 1 n .. , де x  , x n1  b.
1
i
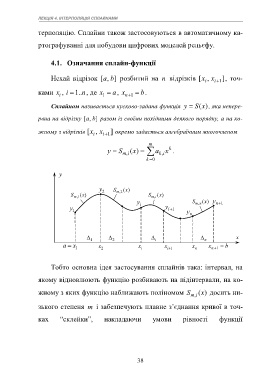
Сплайном називається кусково-задана функція y  S (x ), яка непере-

рвна на відрізку [a , ] b разом із своїми похідними деякого порядку, а на ко-

жному з відрізків [x i , x  i 1 ] окремо задається алгебраїчним многочленом

m
k
a
y  S m, i ( x)   k, i x .
k 0

y

y 2 S m 2 , (x )
S m 1 , (x ) S m ,i (x )
y i S m ,n (x ) y n  1
y y  i 1
1 y
n

    x
1 2 i n
a  x x x x x x  b
1 2 i 1  i n n1

Тобто основна ідея застосування сплайнів така: інтервал, на

якому відновлюють функцію розбивають на підінтервали, на ко-

жному з яких функцію наближають поліномом S m ,i (x ) досить ни-

зького степеня m і забезпечують плавне з’єднання кривої в точ-

ках “склейки”, накладаючи умови рівності функції

38