Page 26 - 4195

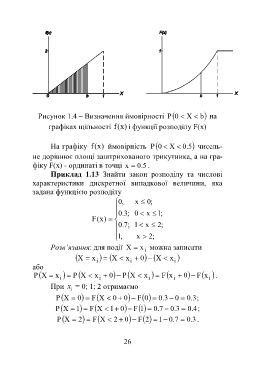
Рисунок 1.4 – Визначення ймовірності 0P  X   b на
графіках щільності x(f ) і функції розподілу F(х)

На графіку (f ) x ймовірність 0P  X   5 . 0 чисель-
не дорівнює площі заштрихованого трикутника, а на гра-
фіку F(х) - ординаті в точці x  5 . 0 .
Приклад 1.13 Знайти закон розподілу та числові
характеристики дискретної випадкової величини, яка
задана функцією розподілу
 ,0 х  ;0
 ; 0  х  ;1
 3.0
) х ( F  
 ; 7 . 0 1  х  ;2
 , 1 х  ;2

Розв’язання: для події X  x можна записати
i
X  x i  X  x  0  X  x i 
i
або
P X  x i   P X  x  0  P X  x i   F x  0  F  x .
i
i
i
При x = 0; 1; 2 отримаємо
i
P X   0  F X  0  0  F   00  3 .  0  ; 3 . 0
P X   1  F X  1 0  F   01  7 .  3 . 0  ; 4 . 0
P X   2  F X  2  0  F   12   7 . 0  3 . 0 .

26