Page 53 - 4162

n(t) n0=const
Реалізація
n (t)1
n (t)2
n (t)3
n (t)4 n (t)4

n (t)6
n (t)7
0 t1 t

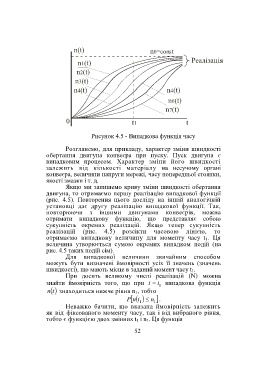
Рисунок 4.5 - Випадкова функція часу

Розглянемо, для прикладу, характер зміни швидкості
обертання двигуна конвеєра при пуску. Пуск двигуна є
випадковим процесом. Характер зміни його швидкості
залежить від кількості матеріалу на несучому органі
конвеєра, величини напруги мережі, часу попередньої стоянки,
якості змазки і т. д.
Якщо ми запишемо криву зміни швидкості обертання
двигуна, то отримаємо першу реалізацію випадкової функції
(рис. 4.5). Повторення цього досліду на іншій аналогічній
установці дає другу реалізацію випадкової функції. Так,
повторюючи з іншими двигунами конвеєрів, можна
отримати випадкову функцію, що представляє собою
сукупність окремих реалізацій. Якщо тепер сукупність
реалізацій (рис. 4.5) розсікти часовою лінією, то
отримаємо випадкову величину для моменту часу t 1. Ця
величина утворюється сумою окремих випадком подій (на
рис. 4.5 таких подій сім).
Для випадкової величини звичайним способом
можуть бути визначені ймовірності усіх її значень (значень
швидкості), що мають місце в заданий момент часу t 1.
При досить великому числі реалізацій (N) можна
знайти ймовірність того, що при t  випадкова функція
t
1
n  t знаходиться нижче рівня n 1, тобто
P n   nt  .
1 1
Неважко бачити, що вказана ймовірність залежить
як від фіксованого моменту часу, так і від вибраного рівня,
тобто є функцією двох змінних t 1 і n 1. Ця функція

52