Page 51 - 4162

події дорівнює xP  x  x    x . Візьмемо відношення
0 0
P x  x  x    x
0 0
.
 x
Границя цього відношення при x  0 називається
густиною ймовірності
P x  x  x    x
p  x  lim 0 0 . (4.6)
 x0  x
Крива, що відображає залежність густини ймовірності
р(х) від параметру х, називається диференційною функцією
розподілу ймовірності. Приблизний вигляд такої функції
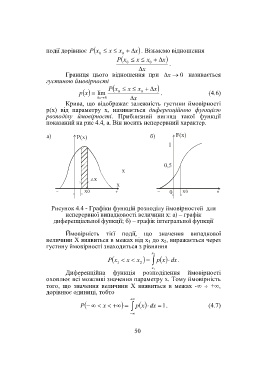
показаний на рис 4.4, а. Він носить неперервний характер.

а) P(x) б) F(x)
1

0,5
x
x
x
x0 0 x0

Рисунок 4.4 - Графіки функцій розподілу ймовірностей для
неперервної випадковості величини х: а) – графік
диференціальної функції; б) – графік інтегральної функції

Ймовірність тієї події, що значення випадкової
величини Х виявиться в межах від х 1 до х 2, виражається через
густину ймовірності знаходиться з рівняння
2 x
P x  x  x    p   dxx .
1 2
1 x
Диференційна функція розподілення ймовірності
охоплює всі можливі значення параметру х. Тому ймовірність
того, що значення величини Х виявиться в межах -  +,
дорівнює одиниці, тобто

P    x      p   dxx  1. (4.7)
 

50