Page 43 - 157

€
2. На графіку зображають значення F N   0x  для x  x min  x ; в
 1
€
точках х (1), х (2),…,x (N)функція F N  x міняється стрибком на величину 1/N.
€
Очевидно, що F N   1x  , коли x  x max  x  N . Якщо деякі елементи вибірки
збігаються між собою, наприклад x  j  x  1j   ... x j r  1 (усього r значень,

€
що збіглися,), то при x = x(j) F N  x функція змінить своє значення на
величину r/N.
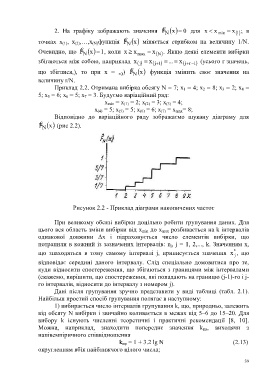
Приклад 2.2. Отримана вибірка обсягу N = 7; x 1 = 4; x 2 = 8; x 3 = 2; x 4 =
5; x 5 = 6; x 6 = 5; x 7 = 3. Будуємо варіаційний ряд:
х min = x (1) = 2; x (2) = 3; x (3) = 4;
x (4) = 5; x (5) = 5; x (6) = 6; x (7) = х max= 8;
Відповідно до варіаційного ряду зображаємо шукану діаграму для
€
F N  x (рис 2.2).

Рисунок 2.2 - Приклад діаграми накопичених частот

При великому обсязі вибірки доцільно робити групування даних. Для
цього вся область зміни вибірки від х min до x max розбивається на k інтервалів
однакової довжини Δх і підраховується число елементів вибірки, що
потрапили в кожний із зазначених інтервалів: n j, j = 1, 2,..., k. Значенням х,
*
що знаходяться в тому самому інтервалі j, приписується значення x , що
j
відповідає середині даного інтервалу. Слід спеціально домовитися про те,
куди відносити спостереження, що збігаються з границями між інтервалами
(скажемо, вирішити, що спостереження, які попадають на границю (j-1)-го і j-
го інтервалів, відносити до інтервалу з номером j).
Дані після групування зручно представити у виді таблиці (табл. 2.1).
Найбільш простий спосіб групування полягає в наступному:
1) вибирається число інтервалів групування k, що, природньо, залежить
від обсягу N вибірки і звичайно коливається в межах від 5–6 до 15–20. Для
вибору k існують численні теоретичні і практичні рекомендації [8, 10].
Можна, наприклад, знаходити попереднє значення k пр, виходячи з
напівемпіричного співвідношення
k пр = 1 + 3.2 lg N (2.13)
округленням вбік найближчого цілого числа;

39