Page 39 - 157

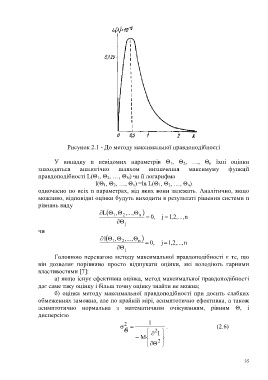
Рисунок 2.1 - До методу максимальної правдоподібності

У випадку n невідомих параметрів Θ 1, Θ 2, …, Θ n їхні оцінки
знаходяться аналогічно шляхом визначення максимуму функції
правдоподібності L(Θ 1, Θ 2, …, Θ N) чи її логарифма
l(Θ 1, Θ 2, …, Θ n) =ln L(Θ 1, Θ 2, …, Θ n)
одночасно по всіх n параметрах, від яких вони залежать. Аналітично, якщо
можливо, відповідні оцінки будуть виходити в результаті рішення системи n
рівнянь виду
  L  , ,..., 
1
2
n
 , 0 j  2 , 1 ,..., n
 
j
чи
  l  , ,..., 
1
n
2
 , 0 j  2 , 1 ,..., n
  j
Головною перевагою методу максимальної правдоподібності є те, що
він дозволяє порівняно просто відшукати оцінки, які володіють гарними
властивостями [7]:
а) якщо існує ефективна оцінка, метод максимальної правдоподібності
дає саме таку оцінку і більш точну оцінку знайти не можна;
б) оцінка методу максимальної правдоподібності при досить слабких

обмеженнях заможна, але по крайній мірі, асимптотично ефективна, а також
асимптотично нормальна з математичним очікуванням, рівним Θ, і
дисперсією
2 1
  . (2.6)
€
  2 
  l

 M  
  2 


35