Page 31 - 157

Приклад 1.3. Двовимірний нормальний розподіл грає настільки ж
велику роль при описі властивостей сукупності двох випадкових величин, як
і одномірний нормальний розподіл для окремих випадкових величин.
Двовимірний нормальний розподіл задається функцією щільності
імовірностей виду
  2
1   1  x  m X 
1

f  ,x 1 x 2   exp  2  1  

2 X  X 1  2  2 1      X 1 


1 2 (1.29)
2  
 x  m   x  m   x  m  
 2  1 X 1   2 X 2    2 X 2    .
         
 X 1   X 2   X 2  
 
П'ять параметрів – математичні очікування m X 1 , m X 2 , дисперсії  ,  X 2
X
1
кожної випадкової величини Х 1, Х 2 і коефіцієнт кореляції ρ = ρ(Х 1, Х 2) –
цілком задають цей розподіл.
Формулу (1.29) можна записати в матричній формі
1  T  1 
1  X C X
f  ,x 1 x 2  e 2 , (1.30)
2 C 2 / 1

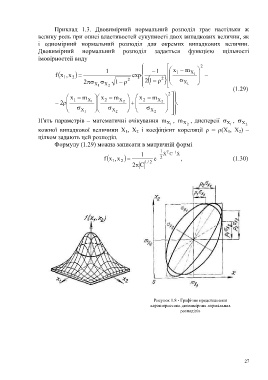
Рисунок 1.8 - Графічне представлення

характеристики двовимірних нормальних
розподілів

27