Page 28 - 157

F(x 1, x 2) = F(x 1) F(x 2) чи f(x 1, x 2) = f(x 1) f(x 2) (1.18)
Аналогічно поняттю умовної імовірності може бути введене поняття
умовного розподілу, наприклад, умовного розподілу випадкової величини Х 1
за умови, що величина Х 2 прийняла деяке конкретне значення a 2:

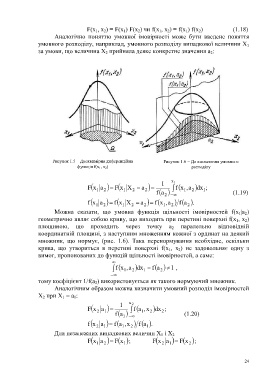
Рисунок 1.5 – Двохвимірна диференційна Рисунок 1.6 – До визначення умовного
функція f(x 1, х 2) розподілу

x
1 1
F x 1 a 2  xF 1 X  a 2   f  ,x 1 a 2 dx 1 ;
2
f  a 2   (1.19)
f x a  xf X  a  f  ,x a   .af
1 2 1 2 2 1 2 2
Можна сказати, що умовна функція щільності імовірностей f(x 1|a 2)
геометрично являє собою криву, що виходить при перетині поверхні f(x 1, x 2)
площиною, що проходить через точку а 2 паралельно відповідній
координатній площині, з наступним множенням кожної з ординат на деякий
множник, що нормує, (рис. 1.6). Така перенормування необхідне, оскільки
крива, що утвориться в перетині поверхні f(x 1, x 2) не задовольняє одну з
вимог, пропонованих до функцій щільності імовірностей, а саме:

 f  ,x 1 a 2 dx  f   1a 2  ,
1
 
тому коефіцієнт 1/f(a 2) використовується як такого нормуючий множник.
Аналогічним образом можна визначити умовний розподіл імовірностей
Х 2 при Х 1 = а 1:
x
1 2
F x 2 a 1   f  ,a 1 x 2 dx 2 ;
f  a 1   (1.20)

f x a  f  ,a x   .af
2 1 1 2 1
Для незалежних випадкових величин X 1 і X 2
F x 1 a 2  F  ; F x 2 a 1  F  ;
x
x
1
2
24