Page 24 - 157

розсіювання випадкової величини (m) і ступінь цього розсіювання (σ X чи
2
 ).
X
2
З визначення математичного очікування m = М{Х} і дисперсії  = D
X
{X} випливають їхні властивості:
М{с} = с; D{c} = 0;
2
М {с X} = с М (X); D{c X} = с D{X}; (1.9)
2
М (а + b X} = а + b М{Х}; D{a + b X} = b D{X},
де а, b, с – деякі константи.
Для характеристики варіабельності випадкової величини іноді
застосовується коефіцієнт варіації δ.
Значення m і σ X використовуються для центрування і нормування
випадкової величини X за допомогою перетворень


X  X  m ; *X  X  m X  X .
X
 X  X

При цьому величина X називається центрованою, a X* – нормованою
0
(стандартизованою) випадковою величиною. Очевидно, що m  ; m  0;

X X *
 X *  1.
Для більш повної оцінки виду функцій розподілу застосовуються
головним чином центральні моменти третього і четвертого порядків. З
їхньою допомогою вводяться характеристики ступеня симетрії і згладженості
кривої функції щільності розподілу f(х) — безрозмірні коефіцієнти асиметрії
γ 1 і ексцесу γ 2 [1].
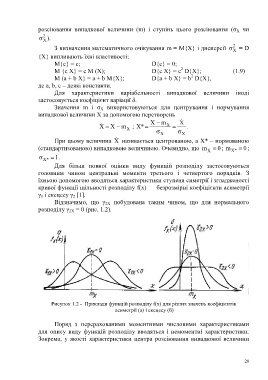
Відзначимо, що γ 2X побудована таким чином, що для нормального
розподілу γ 2X = 0 (рис. 1.2).

Рисунок 1.2 - Приклади функцій розподілу f(x) для різних значень коефіцієнтів
асиметрії (а) і ексцесу (б)

Поряд з перерахованими моментними числовими характеристиками
для опису виду функцій розподілу вводяться і немоментні характеристики.
Зокрема, у якості характеристики центра розсіювання випадкової величини

20