Page 130 - 157

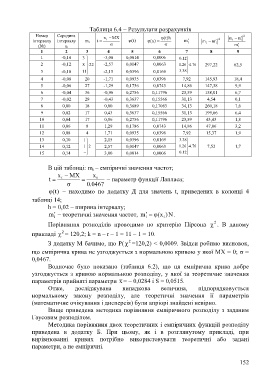
Таблиця 6.4 – Результати розрахунків
Номер Середина x  MX  )t( h m  m 2
2
інтервалу інтервалу m i t  i ) t (   )x(  m m  m i i
i
i
i
(№) х і   m i
1 2 3 4 5 6 7 8 9
1 -0,14 3  -3,00 0,0014 0,0006 . 0 12
 
2 -0,12 8  22 -2,57 0,0147 0,0063 . 1 26  . 4 76 297,22 62,5
3 -0,10 11  -2,15 0,0396 0,0169 . 3 38 


4 -0,08 20 -1,71 0,0935 0,0396 7,92 145,93 18,4
5 -0,06 27 -1,29 0,1736 0,0743 14,86 147,38 9,9
6 -0,04 36 -0,96 0,2756 0,11796 23,59 158,01 6,7
7 -0,02 29 -0,43 0,3637 0,15566 31,13 4,54 0,1
8 0,00 18 0,00 0,3689 0,17063 34,13 260,18 7,6
9 0,02 17 0,43 0,3637 0,15566 31,13 199,66 6,4
10 0,04 17 0,86 0,2756 0,11796 23,59 43,43 1,8
11 0,06 8 1,29 0,1786 0,0743 14,86 47,06 3,2
12 0,08 4 1,71 0,0935 0,0396 7,92 15,37 1,9
13 0,10 1  2,15 0,0396 0,0169 . 3 38
 
14 0,12 1  2 2,57 0,0147 0,0063 . 1 26  . 4 76 7,52 1,7

15 0,14   3,00 0,0014 0,0006 . 0 12 


В цій таблиці: m i – емпіричні значення частот;
x  MX x i
i
t   – параметр функції Лапласа;
 . 0 0467
) t (  – находимо по додатку Д для значень t, приведених в колонці 4

таблиці 14;
h = 0,02 – ширина інтервалу;

m – теоретичні значення частот, m  x (  i ) N .
i
i
2
Порівняння розподілів проводимо по критерію Пірсона  . В даному
2
прикладі  = 120,2; k = n – r – 1 = 11 – 1 = 10.
2
З додатку М бачимо, що Р( =120,2) < 0,0009. Звідси робимо висновок,
що емпірична крива не узгоджується з нормальною кривою у якої МХ = 0;  =
0,0467.
Водночас було показано (таблиця 6.2), що ця емпірична крива добре
узгоджується з кривою нормальною розподілу, у якої за теоретичне значення
параметрів прийняті параметри x = – 0,0284 і S = 0,0515.
Отже, досліджувана випадкова величина, підпорядковується
нормальному закону розподілу, але теоретичні значення її параметрів
(математичне очікування і дисперсія) були апріорі знайдені невірно.
Вище приведена методика порівняння емпіричного розподілу з заданим
Гаусовим розподілом.
Методика порівняння двох теоретичних і емпіричних функцій розподілу
приведена в додатку Б. При цьому, як і в розглянутому прикладі, при
вирівнюванні кривих потрібно використовувати теоретичні або задані
параметри, а не емпіричні.

152