Page 126 - 157

. 0 02 . 0 000758
Наприклад, (P x i )  . 0  0379   . 0 01472.
. 0 0515 . 0 0515
Значення (P x i ) приведені в колонці 7.
Перемноживши P x ( i ) на N   m  200, отримуємо значення частот
i
кривої , виражених по закону Гауса (колонка 8).
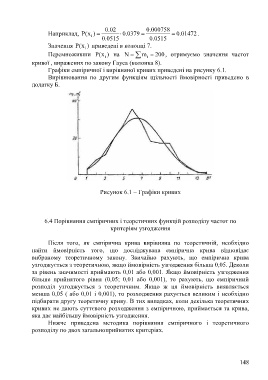
Графіки емпіричної і вирівняної кривих приведені на рисунку 6.1.
Вирівнювання по другим функціям щільності ймовірності приведено в
додатку Б.

Рисунок 6.1 – Графіки кривих

6.4 Порівняння емпіричних і теоретичних функцій розподілу частот по
критеріям узгодження

Після того, як емпірична крива вирівняна по теоретичній, необхідно
найти ймовірність того, що досліджувана емпірична крива відповідає
вибраному теоретичному закону. Звичайно рахують, що емпірична крива
узгоджується з теоретичною, якщо ймовірність узгодження більша 0,05. Деколи
за рівень значимості приймають 0,01 або 0,001. Якщо ймовірність узгодження
більше прийнятого рівня (0,05; 0,01 або 0,001), то рахують, що емпіричний
розподіл узгоджується з теоретичним. Якщо ж ця ймовірність виявляється
менша 0,05 ( або 0,01 і 0,001), то розходження рахується великим і необхідно
підбирати другу теоретичну криву. В тих випадках, коли декілька теоретичних
кривих не дають суттєвого розходження з емпіричною, приймається та крива,
яка дає найбільшу ймовірність узгодження.
Нижче приведена методика порівняння емпіричного і теоретичного
розподілу по двох загальноприйнятих критеріях.

148