Page 128 - 157

6.4.2 Критерій Колмогорова 

Якщо теоретичне значення параметрів відоме, то найкращим критерієм є
критерій Колмогорова . При невідомих параметрах цей критерій також
раціональний, але в цьому випадку він дає завищені оцінки.
Застосування даного критерію розглянемо на цьому ж прикладі.

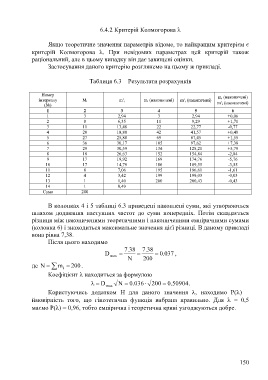
Таблиця 6.3 – Результати розрахунків

Номер
m i (накопичені)
інтервалу M i m i m i (накопичені) m i (накопичені)
(№) m i (накопичені)
1 2 3 4 5 6
1 3 2,94 3 2,94 +0,06
2 8 6,35 11 9,29 +1,71
3 11 13,48 22 22,77 -0,77
4 20 18,80 42 41,57 +0,48
5 27 25,88 69 67,45 +1,55
6 36 30,17 105 97,62 +7,38
7 29 30,59 134 128,21 +5,79
8 18 26,63 152 154,84 -2,84
9 17 19,92 169 174,76 -5,76
10 17 14,79 186 189,55 -3,55
11 8 7,06 195 196,61 -1,61
12 4 3,42 199 199,03 -0,03
13 1 1,40 200 200,43 -0,43
14 1 0,49
Сума 200

В колонках 4 і 5 таблиці 6.3 приведені накоплені суми, які утворюються
шляхом додавання наступних частот до суми попередніх. Потім складається
різниця між накопиченими теоретичними і накопиченими емпіричними сумами
(колонка 6) і знаходиться максимальне значення цієї різниці. В даному прикладі
вона рівна 7,38.
Після цього находимо
. 7 38 . 7 38
D max    . 0 037 ,
N 200
де N   m i  200.
Коефіцієнт  находиться за формулою

  D N  . 0 036 200  . 0 50904.
max
Користуючись додатком Н для даного значення , находимо Р() –
ймовірність того, що гіпотетична функція вибрана правильно. Для  = 0,5

маємо Р() = 0,96, тобто емпірична і теоретична криві узгоджуються добре.

150