Page 99 - 14

102

y(kT) (метод
k ( w kT ) ( y kT ) зворотнього
перетворення
Лапласа)
0 0 0 0
1 0 0 0
2 0.01 0.014 0.014
3 0.016 0.029 0.029
4 0.02 0.049 0.049
5 0.024 0.073 0.073
6 0.027 0.101 0.101
7 0.03 0.131 0.131
8 0.032 0.163 0.163
9 0.034 0.197 0.197
10 0.035 0.232 0.232

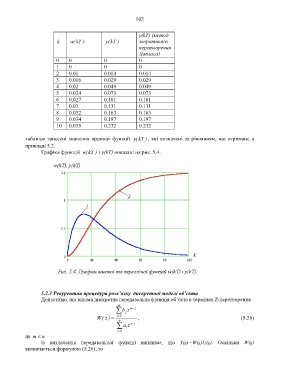
таблицю занесені значення ординат функції (y kT ), які визначені за рівнянням, що отримане в
прикладі 5.2.
Графіки функцій (w kT ) і y(kT) показані на рис. 5.4.

5.2.3 Рекурентна процедура розв’язку дискретної моделі об’єкта
Допустимо, що відома дискретна передавальна функція об’єкта в термінах Z-перетворення
m
 b j z m  j
j 0
W ) z (  , (5.26)
n
 a i z n i
i 0
n
де m 
Із визначення передавальної функції випливає, що Y(z)=W(z)U(z). Оскільки W(z)
визначається формулою (5.26), то