Page 64 - 14

67
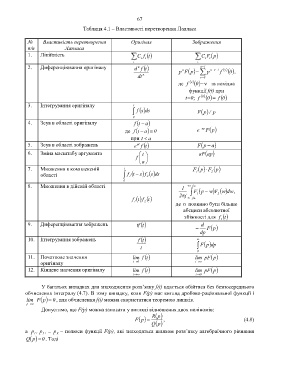
Таблиця 4.1 – Властивості перетворення Лапласа

№ Властивість перетворення Оригінал Зображення
п/п Лапласа
1. Лінійність  C i f i  t  C i F i  p
i i
2. Диференціювання оригіналу d n f  t n 1
p n F  p  p n   1 f     0 ,
dt n  0
де f     0 –та похідна
функції f(t) при
t=0; f  0  0  f  0
3. Інтегрування оригіналу t
 f  dss F   p/p
0
4. Зсув в області оригіналу f t   a
де tf  a  0 e  ap F  p
a
при t 
5. Зсув в області зображень e at f  t F p   a
6. Зміна масштабу аргумента  t  aF  ap
 f 
 a 
7. Множення в комплексній t F 1   Fp  2  p
області  f 1   st   dssf 2
0
8. Множення в дійсній області    j
1
 F 1   wp   dwwF 2 ,
2 j
f 1    tft 2    j
де  повинно бути більше
абсциси абсолютної
збіжності для  tf 1
9. Диференціювання зображень tf  t d
 F   p
dp
10. Інтегрування зображень f  t 
F  dpp
t 
0
11. Початкове значення lim f  t lim pF  p
оригіналу t 0 t 
12. Кінцеве значення оригіналу lim f  t lim pF  p
t  t 0

У багатьох випадках для знаходження розв’язку f(t) вдається обійтися без безпосереднього
обчислення інтегралу (4.7). В тому випадку, коли F(p) має вигляд дробово-раціональної функції і
lim F   0p  , для обчислення f(t) можна скористатися теоремою лишків.
p 
Допустимо, що F(p) можна записати у вигляді відношення двох поліномів:
R  p
  pF  , (4.8)
Q  p
a p 1 , p 2 , ... p – полюси функції F(p), які знаходяться шляхом розв’язку алгебраїчного рівняння
K
Q   0p  . Тоді