Page 60 - 14

63
 
 Y   s   Y   s 
Re s  Re  s  .
    Tsp  
  e1  s   s  d   e1   sp T  
  ds   s 2 
 p  j 
T
Оскільки
d  p s T   p s T
1 e  2   T e 2   T ,
ds s p j T  s p j T 
то
1   2  
Y *   p    jpY  . (3.67)
T     T 
Співвідношення (3.67) характеризує сигнал на виході ключа Кл в частотній області. Воно дає
можливість глибше зрозуміти суть квантування в часі неперервних сигналів. Допустимо, що
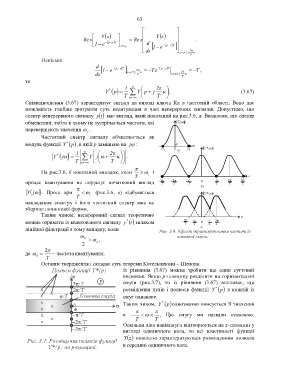
спектр неперервного сигналу  ty має вигляд, який показаний на рис.3.6, а. Вважаємо, що спектр
обмежений, тобто в ньому не зустрічається частоти, які
перевершують значення  .
c
Частотний спектр сигналу обчислюється як
модуль функції  pY * , в якій p заміщено на j :
1    2   
Y *   j     j    .
Y

T      T  

На рис.3.6, б показаний випадок, коли   і
c
T
процес квантування не порушує початковий вигляд

Y  j . Проте при   (рис.3.6, в) відбувається
c
T
накладання спектру і його частотний спектр вже не
зберігає початкової форми.
Таким чином, неперервний сигнал теоретично
можна отримати із квантованого сигналу  ty * шляхом
лінійної фільтрації в тому випадку, коли

0   ,
2 c
 2
де   – частота квантування.
0
T
Останнє твердження і складає суть теореми Котельникова – Шенона.
Із рівняння (3.67) можна зробити ще один суттєвий
висновок. Якщо p-площину розділити на горизонтальні
смуги (рис.3.7), то із рівняння (3.67) випливає, що
розміщення нулів і полюсів функції Y *  p в кожній із
смуг однакове.
Таким чином, Y *  p однозначно описується її значення
 
в     . Цю смугу ми назвали основною.
T T
Оскільки ліва напівсмуга відтворюється на z–площині у
вигляді одиничного кола, то всі властивості функції
Y  z повністю характеризуються розміщенням полюсів
в середині одиничного кола.