Page 56 - 14

59
2.  t 1 1  T 1 e pT z

p e pT  1 z  1
3. t  T 1 e pT z
T T
p 2 pT 2 z   1 2
e   1
4. t  T 2 2 2 pT e pT  1 T 2 z z   1
2
p 3 T e e pT   1 3 z   1 3
t 
5. a a  T 1 e pT z

p  ln  a e pT  a  T z  a  T
6. e  t  e   T 1 e pT z
, d  e   T
p   e pT  d z  d
7. te  t   eT   T 1 Te pT d Tz d 
p   2 e pT   d 2 z   d 2
8. sin 0 t sin   0 T   0 e pT sin 0 T z sin 0 T
2
2
p   2 0 e 2 pT  e 2 pT cos 0 T  1 z  z 2 cos  0 T  1

9. cos 0 T cos   0 T  p e pT e pT  cos 0 T  z z  cos 0 T 
2
p   2 0 e 2 pT  e 2 pT cos 0 T  1 z  z 2 cos 0 T  1
2

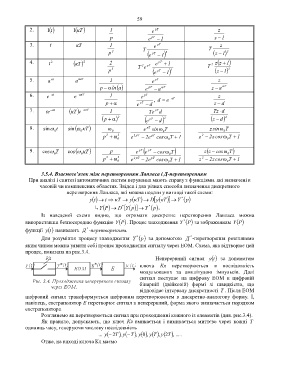
3.5.4. Взаємозв’язок між перетворенням Лапласа і Д-перетворенням
При аналізі і синтезі автоматичних систем керування мають справу з функціями. які визначені в
часовій чи комплексних областях. Звідси і два різних способи визначення дискретного
перетворення Лапласа, які можна подати у вигляді такої схеми:
y  t  t   T  y  T  D y  T  Y *  p
↳  PY  D * Y  p  Y *  p .
Із наведеної схеми видно, що отримати дискретне перетворення Лапласа можна
використавши безпосередню функцію  PY . Процес знаходження  PY * за зображенням  PY
*
функції  ty називають Д -перетворенням.
*
Для розуміння процесу знаходження Y *  p за допомогою Д -перетворення розглянемо
яким чином можна уявити собі процес проходження сигналу через ЕОМ. Схема, яка відтворює цей
процес, показана на рис.3.4.
Неперервний сигнал  ty за допомогою
ключа Кл перетворюється в послідовність
модульованих за амплітудою імпульсів. Далі
сигнал поступає на цифрову ЕОМ в цифровій
бінарній (двійковій) формі зі швидкістю, що
відповідає інтервалу дискретності T . Після ЕОМ
цифровий сигнал трансформується цифровим перетворювачем в дискретно-аналогову форму. І,
накінець, екстраполятор Е перетворює сигнал в неперервний, форма якого визначається порядком
екстраполятора
Розглянемо як перетворюється сигнал при проходженні кожного із елементів (див. рис.3.4).
Як правило, допускають, що ключ Кл вмикається і вимикається миттєво через кожні T
одиниць часу, генеруючи числову послідовність
... y  2T  , y  T        ...,2,,0, y y T y T .
Отже, на виході ключа Кл маємо