Page 81 - 128

R()) зменшується зі збільшенням  і вже при порівняно
невеликих  стає достатньо малою. Інтервал часу від =0 до
= 0, при якому B ф() стає достатньо малою, називають
інтервалом автокореляцій.
Цей інтервал може визначатися по-різному. Іноді його
розраховують як час  , при якому нормована
Автокореляційна функція R() зменшується до визначеного
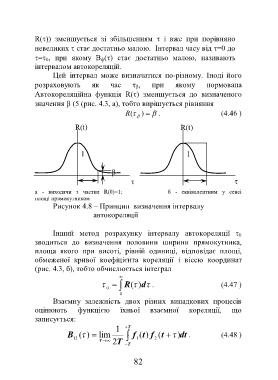
значення  (5 (рис. 4.3, а), тобто вирішується рівняння
( R  )   . (4.46 )

R(t) R(t)

1 1


   


а - виходячи з частки R(0)=1; б - еквівалентним у сенсі
площі прямокутником
Рисунок 4.8 – Принцип визначення інтервалу
автокореляції

Інший метод розрахунку інтервалу автокореляції  0
зводиться до визначення половини ширини прямокутника,
площа якого при висоті, рівній одиниці, відповідає площі,
обмеженої кривої коефіцієнта кореляції і віссю координат
(рис. 4.3, б), тобто обчислюється інтеграл

  R ( ) d . (4.47 )

0
0
Взаємну залежність двох різних випадкових процесів
оцінюють функцією їхньої взаємної кореляції, що
записується:
1  T
B ( )  lim  f ( t) f ( t  ) dt . (4.48 )
12 1 2
T  2 T  T

82