Page 65 - 6832

k
N = 2 + 2 k + 1.
Відмітимо, що число дослідів, визначене цим співвідношенням, суттєво менше ніж, наприклад, у
k
плані ПФЕ 3 при k>2.

Таблиця 4.9
Кількість коефіцієнтів Число дослідів при плані
квадратичного
Кількість полінома ПФЕ 2 , ПФЕ 3 , Другого
k
k
факторів k kl k k порядку,
S 1 k 2  N  2 N  3 N  2  2  1
k
k
2 l( k  l ) 2
1 3 2 3 3
2 6 4 9 9
3 10 8 27 15
4 15 16 81 25
5 21 32 244 43
6 28 64 732 77
7 36 128 2196 143

9 Ортогональні центрально-композиційні плани

Обробка даних експерименту пов’язана з вирішенням досить громіздкої системи нормальних
k
рівнянь. Щоб запобігти цьому добудову ПФЕ 2 (вибір положення з іркових точок) треба робити
таким чином, щоб виконувались принципи ортогональності і симетрії. Умови нормування можуть не
додержуватися. План другого порядку, задовольняючи і цим умовам, прийнято називати
ортогональним центрально-композиційним планом (ОЦКП).

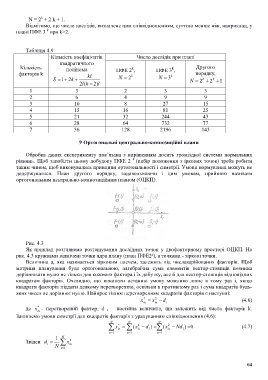
Рис. 4.3
Як приклад розглянемо розташування дослідних точок у двофакторному просторі ОЦКП. На
рис. 4.3 кружками відмічені точки ядра плану (план ПФЕ2²), а точками - зіркові точки.
Величина a, яка називається зірковим плечем, залежить від числаварійованих факторів. Щоб
матриця планування була ортогональною, алгебраїчна сума елементів вектор-стовпців повинна
дорівнювати нулю не тільки для кожного фактора і їх добутку, але й для вектор-стовпців відповідних
квадратам факторів. Очевидно, що виконати останню умову можливо лише в тому раз і, якщо
квадрати факторів піддати деякому перетворенню, оскільки в противному раз і сума квадратів будь-
яких чисел не дорівнює нулю. Найпрос тішим перетворенням квадратів факторів є наступні:
*
2
x  x  d (4.6)
iu iu i
*
де x - перетворений фактор; d i – постійна величина, що залежить від числа факторів k.
iu
Запишемо умови симетрії для квадратів факторів з урахуванням співвідношення (4.6):
N N N
*
2
 x iu   (x iu  d i )   (x iu 2  Nd i )  0 (4.7)
u 1  u  1 u 1 
1 N
2
Звідси d   x
i iu
N u 1
64