Page 64 - 6832

(дрібною реплікою). Такий план являє собою частину плану ПФЕ. Наприклад, для випадку
вивчення трьох факторів матриця планування ПФЕ 2³ має вигляд, показаний в табл. 4.8.
План ПФЕ 2² тут обведено рамкою.
При нехтуванні ефектом взаємодії вектор-стовпець x 1 x 2 плану ПФЕ 2² можна використовувати
для введення в цей план нового фактора x 3 , що дозволяє визначити лінійну модель об’єкта у вигляді
Y=b 0+b 1x 1+ b 2x 2+ b 3x 3
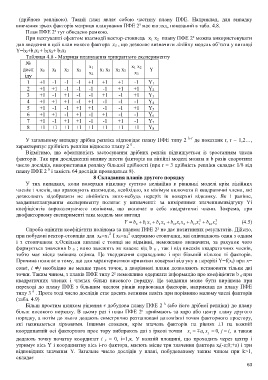
Таблиця 4.8 - Матриця планування трикратного експерименту
№ x 1 x 1 x 2
досл x 0 x 1 x 2 x 3 x 2 x 1 x 3 x 2 x 3 x 3 Y
іду
1 +1 -1 -1 -1 +1 +1 +1 -1 Y 1
2 +1 +1 -1 -1 -1 -1 +1 +1 Y 2
3 +1 -1 +1 -1 -1 +1 -1 +1 Y 3
4 +1 +1 +1 -1 +1 -1 -1 -1 Y 4
5 +1 -1 -1 +1 +1 -1 -1 +1 Y 5
6 +1 +1 -1 +1 -1 +1 -1 -1 Y 6
7 +1 -1 +1 +1 -1 -1 +1 -1 Y 7
8 +1 +1 +1 +1 +1 +1 +1 +1 Y 8

k-r
У загальному випадку дрібна репліка відповідає плану ПФЕ типу 2 де показник r, r = 1,2…,
k
характеризує дрібність репліки відносно плану 2 .
Відмітимо, що ефективність застосування дрібних реплік підвищується із зростанням числа
факторів. Так при дослідженні впливу шести факторів на лінійні моделі можна в b разів скоротити
число дослідів, використавши репліку більшої дрібності (при r = 3 дрібність репліки складає 1/8 від
6
плану ПФЕ 2 і замість 64 дослідів проводяться 8).
8 Складання планів другого порядку
У тих випадках, коли поверхня відклику суттєво нелінійна в рівнянні моделі крім лінійних
членів і членів, що враховують взаємодію, необхідно, як мінімум включати й квадратичні члени, які
дозволяють відобразити не лінійність яких-небудь переріз ів поверхні відклику. Як і раніше,
завданняпланування експерименту полягає у визначенні: за виміряними значеннямивідгуку Yі
коефіцієнтів апроксимуючого полінома, що включає в себе квадратичні члени. Зокрема, при
двофакторному експерименті така модель має вигляд
2
2
Y  b  b x  b x  b x x  b x  b x (4.5)
0 1 1 2 2 12 1 2 11 1 22 2
Спроба оцінити коефіцієнти полінома за планом ПФЕ 2² не дає позитивних результатів. Дійсно,
2 2
при побудові вектор-стовпців для x 4=x 1 I x 5=x 2 одержимо стовпчики, які співпадають один з одним
і з стовпчиком x.Оскільки вказані с товпці не відмінні, неможливо визначити, за рахунок чого
формується значення b 0 ; воно залежить як власне від b 0 , так і від внесків квадратичних членів,
тобто має місце змішана оцінка. Це твердження справедливе і при більшій кількос ті факторів.
Причина полягає в тому, що для характеристики кривизни поверхні відгуку в перерізі Y=f(x i) при x=
const, i ≠j необхідно не менше трьох точок, а дворівневі плани дозволяють встановити тільки дві
точки. Таким чином, з планів ПФЕ типу 2² неможливо одержати інформацію про коефіцієнти b ii при
квадратичних членах і членах більш високого порядку. Це завдання може бути вирішена при
переході до плану ПФЕ з більшим числом рівнів варіювання факторів, наприклад до плану ПФЕ
k
типу 3 . Проте тоді число дослідів стає досить великим навіть при порівняно малому числі факторів
(табл. 4.9)
k
Більш простим шляхом рішення є добудова плану ПФЕ 2 (або його дрібної репліки) до плану
більш високого порядку. В цьому раз і план ПФЕ 2ⁿ приймають за ядро або центр плану другого
порядку, а потім до нього додають симетрично розташовані допоміжні точки факторного простору,
які називаються зірковими. Іншими словами, крім значень факторів на рівнях ±1 на кожній
координатній осі факторного прос тору вибирають дві з іркові точки x   a , x  , 0 j  , i а також
i j
додають точку початку координат i x = 0, і=1,к. У кожній площині, що проходить через центр і
утримує вісь Y і координатну вісь і-го фактора, маєють місце три значення фактора x i(-a;0;+a) і три
відповідних значення Y. Загальне число дослідів у плані, побудованому таким чином при k>1,
складає
63