Page 10 - 6639
P. 10
1. За означенням ⃗ = ⃗/ . Звідки ⃗ = ⃗ = ⃗ (1 − / ) .
Проінтегрувавши це рівняння за часом від 0 до , отримаємо
∆ ⃗ = ⃗ (1 − /2 ).
2. Шлях , який пройшла частинка за час , визначається як
= ,
де – модуль вектора ⃗. В даному випадку
(1 − / ), якщо ≤ ,
= |1 − / | = ( / − 1), якщо ≥ .
Звідси видно, що при > інтеграл для обчислення шляху необхідно
розбити на дві частини: від 0 до і від до . Інтегруючи, отримаємо
(1 − /2 ), якщо ≤ ,
= 1
(1 + (1 − / ) ), якщо ≥ .
2
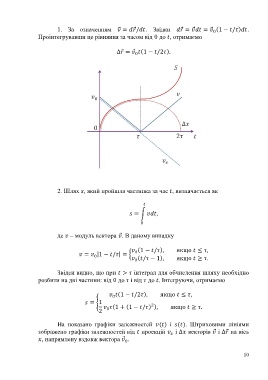
На показано графіки залежностей ( ) і ( ). Штриховими лініями
зображено графіки залежностей від проекцій і ∆ векторів ⃗ і ∆ ⃗ на вісь
, напрямлену вздовж вектора ⃗ .
10