Page 110 - 6285

Вважаючи для завдань середньої складності  0 = 1, а для сту-

дента із середнім рівнем знань  0 = 1 і підставляючи ці значення
до (3.11), встановлюємо, що значення імовірності правильного
виконання в такому випадку P(, )  0,5. Виходячи з цього ма-

сштаб шкали абсцис на рис. 3.14 обрано таким чином, що проекція

точки  0 = 1 на характеристичну криву відповідає величині імові-
рності правильної відповіді, що дорівнює 0,5 за шкалою ординат.

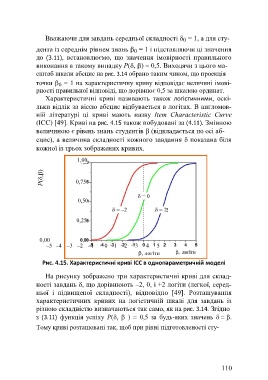
Характеристичні криві називають також логістичними, оскі-
льки відлік за віссю абсцис відбуваеться в логітах. В англомов-
ній літературі ці криві мають назву Item Characteristic Curve
(ICC) [49]. Криві на рис. 4.15 також побудовані за (4.11). Змінною
величиною є рівень знань студентів  (відкладається по осі аб-
сцис), а величина складності кожного завдання  показана біля
кожної із трьох зображених кривих.

1,00

P(,) 0,75

 = 0
0,50

 = –2 = 2

0,25

0,00
–5 –4 –3 –2 –1 0 1 2 3 4 5

, логіти

Рис. 4.15. Характеристичні криві ICC в однопараметричній моделі

На рисунку зображено три характеристичні криві для склад-
ності завдань , що дорівнюють –2, 0, і +2 логіти (легкої, серед-
ньої і підвищеної складності), відповідно [49]. Розташування
характеристичних кривих на логістичній шкалі для завдань із
різною складністю визначаються так само, як на рис. 3.14. Згідно

з (3.11) функція успіху P(,  )  0,5 за будь-яких значень .
Тому криві розташовані так, щоб при рівні підготовленості сту-

110